The Condorcet-IRV voting method is a combination of instant-runoff voting (IRV) and the Condorcet winner criterion. In order to explain it, we must first understand these two things.
The idea of instant-runoff voting is that in an election between three or more candidates, a mere plurality of the vote should not be enough to decide the winner. When no candidate has an absolute majority (i.e. more than 50%) of the vote, there needs to be a runoff — but not just between the top two candidates, eliminating all other contenders at once (as is typical in runoff elections). Instead, in each round, only the worst-performing candidate is eliminated. This means that it may take several rounds before a majority winner is determined.
To facilitate this process, which would be a big hassle (and very expensive) if voters had to go back to the polls for each round, voters list their preferences, from highest to lowest, on their ballots. They may list one, some, or all of the candidates. If a voter’s ballot only lists some of the candidates, and they are all eliminated, the ballot is considered “exhausted” and the voter abstains in all subsequent rounds.
In the first round, all voters’ votes go to their top preference. In the case of no majority winner, the last-place candidate is eliminated, and those voters who went for that candidate have their votes transferred to their next preference, as listed on their ballot. Then another round of tallying begins with the new vote counts. The process is illustrated by this flowchart:
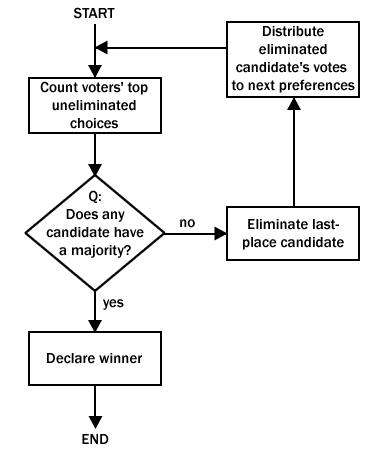
Having explained IRV, we now turn to the Condorcet (pronounced “con-dor-say”) winner criterion (or simply Condorcet criterion), which is a test for evaluating a voting method. Given a set of ballots ranked by preference (as explained above), a Condorcet winner is any candidate who is preferred by a majority of voters in all pairwise comparisons between candidates. That is, suppose you construct a matrix of all candidates “X” vs. every other candidate “Y”, where each entry is the number of voters who rank X higher than Y. For example, let’s say there’s a race between three candidates, A, B, and C, and that the ballots are as follows:
- 2 ballots: A>B>C (meaning A is ranked highest, followed by B, then C)
- 1 ballot: A>C>B
- 3 ballots: B>A>C
- 1 ballot: B>C>A
- 3 ballots: C>A>B
- 1 ballot: C>B>A
Based on these ballots, we can construct the matrix of pairwise comparisons like this:
| candidate | vs. A | vs. B | vs. C |
|---|---|---|---|
| A | — | 6 | 6 |
| B | 5 | — | 6 |
| C | 5 | 5 | — |
Notice that A is preferred to B by 6 out of 11 voters (those in groups 1, 2, and 5), and also preferred to C by 6 out of 11 (groups 1, 2, and 3) — a majority in both cases. So A wins all pairwise comparisons, and is the Condorcet winner of this election. According to the Condorcet criterion, A should be elected. Some voting methods do not necessarily elect A; these are said to fail the test. Any voting method which guarantees that a Condorcet winner wins the election satisfies the criterion, and is known as a “Condorcet method”.
But a Condorcet winner does not always exist. Although for an individual voter, transitivity of preferences generally holds true (that is, if I prefer A over B, and B over C, then I also prefer A over C), it does not hold true at the group level — something known as the Condorcet paradox. When a Condorcet winner does not exist, the criterion doesn’t apply. Voting methods differ on how to choose a winner in such a case. As long as it never fails to elect a Condorcet winner when one exists, a voting method can be considered a Condorcet method.
IRV does not satisfy the Condorcet criterion. In the example above, A would be eliminated first under IRV rules, because he has only 3 first-choice votes whereas B and C both have 4. B would then win the election in the second round. Outcomes under IRV depend heavily on the order of elimination.
However, we can define a modification of IRV which does satisfy Condorcet — let’s call it “Condorcet-IRV”. (It has also been known by other names, such as “Woodall’s Smith+IRV method” [or “WoodSIRV”] and “Benham’s method”.) The procedure follows the same basic outline as IRV, with rank-ordered ballots, multiple rounds of tallying, and redistribution of votes when candidates are eliminated. The difference is that if the candidate to be eliminated under IRV rules is a Condorcet winner, then instead of that candidate being eliminated, the second-to-last-place candidate is. (Note: it can be proven that any candidate who emerges in a particular round of tallying as a Condorcet winner will never cease to be such, and therefore will always win the election under this method. So a shortcut can be taken whenever a Condorcet winner is found.)
In the example above, A appears to be something of a consensus candidate — a “centrist”, perhaps: note that he is the first or second choice of an overwhelming 9 out of 11 voters. IRV fails to promote consensus candidates — it suffers from what some have called the “center squeeze” pathology, with centrist candidates at risk of being squeezed out. (For a real-world example, see the 2009 mayoral election in Burlington, Vermont.) Condorcet-IRV addresses this shortcoming.
When electing one winner from a choice of many candidates, consensus is important — so we should consider whether a voting method satisfies the Condorcet criterion. That’s why the political scientists Richard G. Niemi and William H. Riker, in an article entitled “The Choice of Voting Systems” (Scientific American, June 1976), recommend it over the Borda count. “In our judgment,” they write, “the Condorcet standard is more likely than the Borda one to give rise to a consensus, since the Borda standard can easily leave a majority of the voters dissatisfied with the outcome.”
There is no perfect voting method. But I believe Condorcet-IRV is one of the very best methods for single-winner elections.
Addendum: Tie-breaking rules
On the rare occasions when a tie occurs, we need some extra rules. Different rules can be used for different versions of Condorcet-IRV. I suggest the following:
1. If, in a given round, we find no majority winner or Condorcet winner, and thus need to eliminate the last-place candidate, and two or more are tied for last place, then eliminate all last-place candidates and redistribute their votes at the same time — unless all candidates are tied: in that case, choose one at random to eliminate.
2. If, in a final round between two candidates, they are tied, the winner is the one with more first-preference votes. If these are the same, then add second-preference votes; the winner is the one with the higher total. If still the same, add third-preference votes and so on. If there is still a tie after all (i.e. first through Nth) preferences have been added, then choose the winner at random.
PS: A discussion group I’m a part of recently voted to choose a new video series to watch when we’ve finished our current series, and we used Condorcet-IRV. I recorded the votes and tallying in a Google document.
